Vector Algebra Worksheets Results
Vector Algebra - University of Utah
Vector Algebra x 13.1. Basic Concepts A vector V in the plane or in space is an arrow: it is determined by its length, denoted j V and its direction. Two arrows represent the same vector if they have the same length and are parallel (see figure 13.1). We use vectors to represent entities which are described by magnitude and direction. For example,
https://url.theworksheets.com/3kc4189 Downloads
Preview and Download !


VECTORS WORKSHEETS pg 1 of 13 VECTORS - mrwaynesclass.com
14 Calculate the magnitude of any vector’s horizontal and vertical components. 15 Draw a vector’s horizontal and vertical components. 16 Use trig to calculate a vector’s direction. 17 Calculate a vectors direction as a degree measurement combined with compass directions. 18 Calculate a vector’s magnitude using trig or Pythagorean theorem.
https://url.theworksheets.com/8iw247 Downloads
Preview and Download !


VECTOR ALGEBRA 1 Introduction - University of California, San Diego
VECTOR ALGEBRA 1 Introduction Vector algebra is necessary in order to learn vector calculus. We are deal-ing with vectors in three-dimensional space so they have three components. The number of spatial variables that functions and vector components can depend on is therefore also three. I assume that the reader is familiar with vector addition and subtraction
https://url.theworksheets.com/50pz102 Downloads
Preview and Download !


Vector Algebra - Vancouver Community College
so long as the size and direction of the vector is maintained. The sum of a series of vectors is drawn as the arrow with its tail at the location of the tail of the first vector, and its head at the head of the last vector. A vector that is the sum of other vectors is often called the resultant. We don’t ever really subtract vectors.
https://url.theworksheets.com/5hwt110 Downloads
Preview and Download !
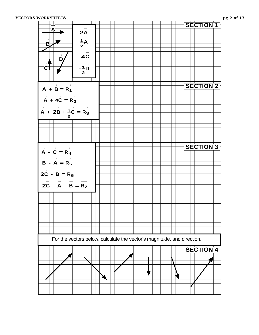
Chapter 10 Vector Algebra Worksheet 1 - Atomic Energy Education Society
Chapter – 10 : Vector Algebra Worksheet ‐ 1 1. Find a unit vector in the direction of a ,⃗ = 3î - 2 ĵ + 6 k à . 2. Find the angle between the vectors a ,⃗= î + ĵ + k à and b ,⃗= î - ĵ +k à. 3. If l a ,⃗ l = √3 , l b ,⃗ l = 2 and a ,⃗.b ,⃗ = 3, Find angle between a ,⃗ and b ,⃗. 4. Write the value of (ı̂.
https://url.theworksheets.com/6fcx87 Downloads
Preview and Download !


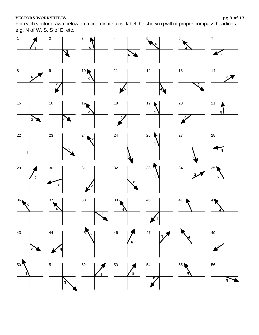
Chapter 10 Vector Algebra Worksheet 3 - Atomic Energy Education Society
10. The magnitude of the vector product of the vector î + ĵ +k à with a unit vector along the sum of vectors 2î +4 ĵ -5k à and λî E2 ĵ 3 k à is equal to √2 . Find the value of λ . 11. Show that four points with position vectors 4î +5 ĵ+k à, - ĵ - k à , 3î +9 ĵ+4 k à and - 4î + 4 ĵ +4k à
https://url.theworksheets.com/5hx9105 Downloads
Preview and Download !
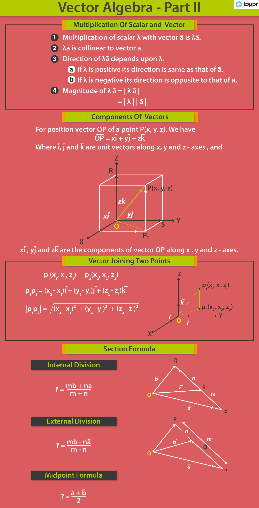

TOPIC 9 VECTOR ALGEBRA
VECTOR ALGEBRA SCHEMATIC DIAGRAM Topic Concept Degree of importance Refrence NCERT Text Book Edition 2007 Vector algebra (i)Vector and scalars * Q2 pg428 (ii)Direction ratio and direction cosines * Q 12,13 pg 440 (iii)Unit vector * * Ex 6,8 Pg 436 (iv)Position vector of a point and collinear vectors * * Q 15 Pg 440 , Q 11Pg440 , Q 16
https://url.theworksheets.com/6fcy80 Downloads
Preview and Download !


1 - Introduction to Vectors - University of Kentucky
Basic Vector Algebra in 1. Vector Equality: Two vectors and are equal if and only if and . 2. Vector Addition: The sum of the vectors and is defined by. 3. Scalar Multiplication: Suppose is a vector and . Then the scalar product of is defined by. Example Find the sum of the following vectors. 1. , 2. ,
https://url.theworksheets.com/2x32170 Downloads
Preview and Download !

Vector Worksheet - Millersburg Area School District
Directions: Solve the following problems algebraically on a separate sheet of paper. 17. A hiker walks 4.5 km in one direction, then makes a 45˚ turn to the right and walks another 6.4 km. What is the magnitude of her displacement?
https://url.theworksheets.com/4kgx105 Downloads
Preview and Download !


Chapter 10 Vector Algebra Worksheet 2 - Atomic Energy Education Society
Chapter – 10 : Vector Algebra Worksheet – 2 1. What is the cosine of the angle ,which the vector î + ĵ + k à makes with y-axis ? 2. If l a ,⃗ l = √3 , l b ,⃗ l = 2 and angle between a ,⃗ and b ,⃗ is 60 4 3. If a , ,⃗ L 2 áı ȷ̂ E3k à and b ,⃗ L 3ı̂ȷ̂ F2k à then find angle between a ,⃗ Eb ,⃗ and a ,⃗ Fb ,⃗ . 4.
https://url.theworksheets.com/5hwv97 Downloads
Preview and Download !


Next results >>